Elution Dynamics of Adsorption: Comparing the Solutions of Direct and Inverse Problems

  JUNIPER PUBLISHERS- ACADEMIC JOURNAL OF POLYMER SCIENCE

Abstract

Studies of the elution dynamics of adsorption have revealed a close correspondence between the analytical solutions to (i) a direct problem formulated using an equilibrium adsorption layer model and (ii) an inverse problem formulated using the method of moments.

Keywords: Elution Dynamics; Adsorption; Charcoal; chromatograph; Numerical Equations

Introduction

The effects of adsorption dynamics on the elution peak profile for an arbitrary adsorption isotherm were previously analyzed in [1] using numerical simulations based on a model that assumed a layer of equilibrium adsorption (LEA model) [2]. Assuming linear adsorption dynamics, [1] revealed that the elution curves simulated using the LEA model agreed well with experimental data obtained for a given integer unit of relative adsorbent bed length (n). The solution parameters to the inverse problem, formulated using the method of moments for integer numbers [3] and expressed in units of relative adsorbent bed length, was found to correspond to the retention and spreading parameters in the LEA model simulation studies. For example, the adsorption dynamics of ethyl chloride on activated charcoal (with bed lengths of 1 and 5 in n units) [4] or halogen hydrocarbons on activated charcoal (n = 1, 2, 3) [5] were found to agree. In parallel, the analysis of elution curves measured from non-unitary adsorbent beds (n = 0.78, 1.54, etc.) by the method of moments [5] was also found to agree with the results obtained from integer-length beds. Solutions to the discrete LEA model use equations that include a factorial term. Previously, solutions to the direct adsorption dynamics problems formulated using the LEA model [6] were shown to be applicable over the real numbers n if the factorial term in the elution curve equation was approximated by the gamma function. The purpose of this study was to compare the solutions of the direct and inverse problems associated with the adsorption dynamics, formulated in terms of the LEA model and method of moments, respectively.

Discussion

The elution curve in the LEA model can be described as [1]

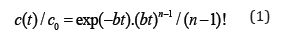
where c(t) is the concentration on the adsorbent bed, equal to n, t is time, n=L/Le is the relative length of the adsorbent bed, L is the absolute length of the bed, Le is the effective kinetic constant of the LEA model, c0 is the maximal concentration determined by the amount of solute added, .)/(1ebuL=+Γ, u is the linear velocity of the mobile phase, and Γ is Henry’s adsorption constant. An equation similar to (1) has been applied in plate theory [7] and may be used to describe chromatographic processes under the approximation that n→∞, for concentration functions represented by a Gaussian curve. Equation (1) differs from most equations used in plate theory because n-1 is taken to be the exponent and the factorial, in place of n. The method of moments [3] was proposed as a method for solving the inverse chromatography problem, and it is used in many techniques, such as statistics. The use of this method in modeling adsorption dynamics proposes calculation of two statistical moments. A first equation is used to define the position of the center of gravity tc of the experimental curve,

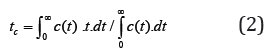
where time tc defines the adsorption Henry’s constant.

A second central moment μ2 is defined by deviations and provides a measure of the spread in the experimental curve,

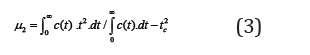
The mathematical equality 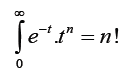along with equation (1) easily yields an expression for the moments in the LEA model,namely

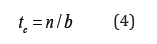
and

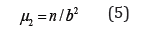
These equations are described here for the first time and were verified by comparison with experimental data.

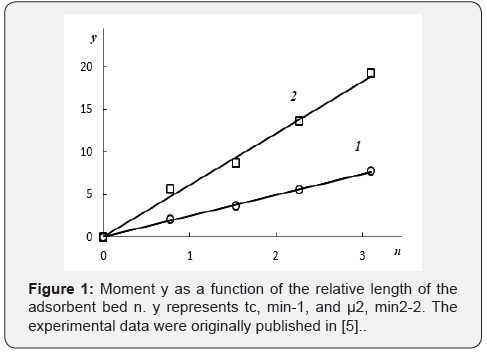
(Figure 1) plots the values of tc and μ2 , calculated as reported previously [5] from the experimental elution profiles corresponding to the adsorption of CF3Cl on activated charcoal beds of varying lengths. The curves shown in (Figure 1) were fit using a linear approximation to yield the equations:

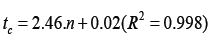
The slopes of these numerical equations were given by b, and in all cases were found to be equal to b= 0.41.

Recently the same data were analyzed without points tc and μ2 at n=0 [8]. The result of approximation is not differed strongly: 2.46. 0.02( 2 0.998) c t= n + R =and μ2 = 6.04.n + 0.12(R2 = 0.993) and in all cases b= 0.41. These results demonstrated that the LEA model and the method of moments are homologous, and they describe and predict the linear adsorption dynamics, including for adsorbent beds of short length.

For more Open Access Journals in Juniper Publishers please click on: https://juniperpublishers.com/

For more articles in  Academic Journal of Polymer Science please click on: https://juniperpublishers.com/ajop/index.php

For more about Juniper Publishers Please click on: https://juniperpublishersblog.wordpress.com/