A Novel Empirical Approach to Estimate the Acoustic Properties of Smart Materials: Part I-Juniper Publishers
Authored
by Francesca Nanni
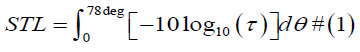
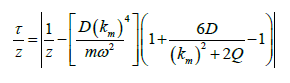
With:
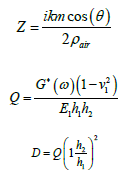
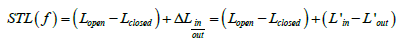
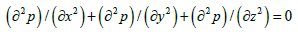
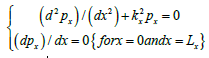
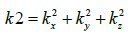
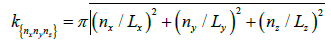
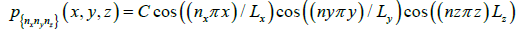
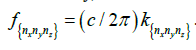

and the variation in frequency

of the Δf -nth eigen mode from the average value, this last constraint imposes the minimization of the index

, indicating the homogeneity in the distance between different mode shapes.

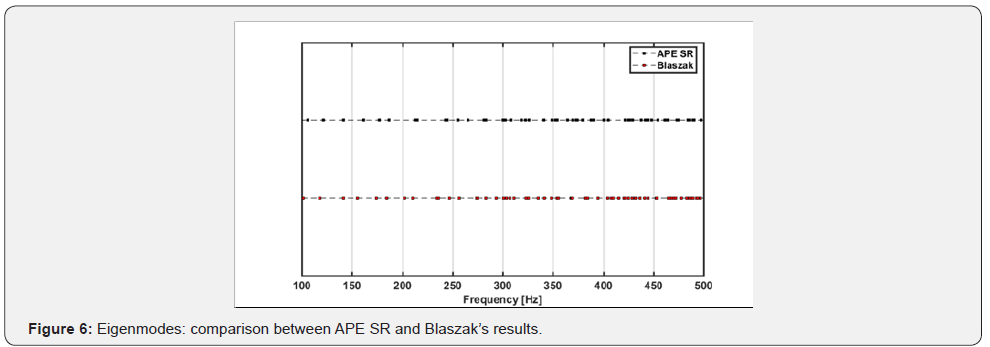






is represented as a bold black line in the graph.


Abstract
In this work, a novel empirical approach to the
estimation of the rheological behaviour of smart materials from the
sound insulation capabilities is proposed. The testing protocol relies
on a small sound research facility that was designed with the goal of
achieving a movable yet flexible measurement system, suitable for both
laboratory environments and quality assurance departments.
Unlike other test protocols relying on lightweight
acoustic research solutions, the proposed methodology was developed to
perform acoustic tests in a diffused field environment, a test condition
much closer to real life applications, and in a sufficiently wide
frequency range (eg. 2 -10kHz).
The proposed test methodology was validated by means
of modal analysis of the chamber and by comparison between empirical
acoustical test results (insertion loss) and the expected theoretical
results.
At last, as a proof of concept, it is showed how to
apply the proposed protocol to the measurement of the sound insulation
of a novel laminate containing a nano composite core and how to evaluate
indirectly the rheological behaviour merely from acoustical data.
Keywords: Acoustics; QA; Smart materials; Sound-insulation
Introduction
The development of Smart materials, composite systems
capable of altering their properties when subjected to external
stimuli, has brought about a revolution in materials science and in
modern society as a whole. In fact, smart materials can be designed
basing on the requirements of a particular application and the response
can be tailored up to the customer’s needs, thus allowing engineers to
develop materials with many different functions embedded.
The alteration can be triggered either by means of
autonomous modifications in the microstructure of the material (passive
smart materials) or by means of external control systems (active or
semi-active smart materials). The first class is based on non-Newtonian
fluids such as Shear-thickening fluids, while the latter on magneto
rheological and electro rheological fluids.
In particular, as smart materials can alter their
vibration damping properties, they prove to be particularly interesting
for acoustic applications in the aeronautical and automotive field, in
which the acoustic comfort of the cabin interior is a major concern.
These advanced composites usually comprise
non-Newtonian fluids encapsulated in a stiffer medium. In particular, as
most smart materials are used in lightweight structures such as
sandwich panels, smart materials are usually interposed as the core of
laminates in constrained layer damping (CLD) configuration.
Furthermore, active or semi-active smart materials
allow for the optimization of the performance of the material for a wide
range of working conditions, as the associated control system modifies
the acoustical response. The acoustical response of Smart materials is
heavily influenced by the rheological response of non-Newtonian fluids
at acoustically significant frequencies,
typically in the kHz range. In practice, in order to evaluate the
acoustical performance of a newly developed Smart material,
as the maximum oscillation frequency of the most commonly
available rheometers is less than 16Hz, regression methods to
derive the high-frequency data from low-frequency rheological
data must be employed.
These methods solve an ill-posed mathematical problem
(Tikhonoff inverse problem), where acoustical data must be
extrapolated from experimental rheological measurements with
an unknown error [1,2]. These numerical methods to evaluate the
acoustical response of smart materials, although tempting, are
still undergoing intensive studies in various fields of research and
typically require massive rheological experimental campaigns
and the solvers are CPU intensive. In the second instance, these
numerical methods only provide a first good estimate of the
acoustical properties of the core, as the acoustical properties of
the smart material are dependent on the boundaries and loads
applied on the full structure.
As a consequence, as R&D laboratories often present the
necessity of testing the outputs of the research right after the
chemical synthesis of the material, it is desirable to find an
empirical approach to provide a preliminary good estimation of
the acoustical properties of the final sandwich structure.
Furthermore, as shown in previous works [3], sound
transmission loss or insertion loss tests can be used as an
alternative to other non-destructive tests (NDT) and can provide
valuable information concerning the mechanical properties of
CLD structures and structures that present adhesive joints or
other permanent bonds as well.
In the following, a novel empirical approach to the evaluation
of the sound insulation properties of smart materials will be
proposed. This method will rely on the design of an Acoustic
Properties Evaluation-Small Room Facility (APESR facility).
The whole leitmotiv of the proposed design procedure relies
on the extension of the measurable frequency range, the weight
reduction of the structure and the maximisation of the versatility
of the facility itself. Secondarily, the APE SR facility was designed
in a modular way, with the possibility of joining it with another
reverberation chamber or anechoic chamber.
This design choice in the future, can allow for changes in the
sound test layout. Finally, it was taken into account the possibility
of attaching a shaker [4,5], for forced-response vibroacoustic
tests. In fact, during the design process, it was considered the
necessity of achieving a sound research facility suitable for
addressing both sound transmission loss and sound absorption
loss, respectively by means of insertion loss (and/or transmission
loss) test evaluations and sound absorption test evaluations.
While traditional sound transmission loss tests performed
in standardized facilities require non-negligible amounts of
materials for the test samples (up to 6square meters), the APE SR
facility was designed trying to minimize the amount of material
necessary for each test. ISO A3 samples were considered as a
reasonable compromise between good measurements (the larger
the sample, the better) and typical laboratory material production
rates.
On the other hand, even though standard laboratory tests like
the ones performed by using impedance tubes [6], require small
samples, they only allow normal incidence sound fields and very
narrow frequency bandwidths. Therefore, the design of the main
body of the reverberation chamber is characterised by some main
critical factors: volume of the acoustical cavity, shape of the cavity,
surface finish of the internal surface and effect of the closing wall.
The interior volume of the small reverberation chamber
introduces limitations as far as the analysis at lower frequencies
is regarded. This can be traced back to the modal response of the
air volume, characterized by highly superposed and singularly
undistinguishable modes. The lower limit to the beginning of this
chaotic dynamic response is given by the Schroeder frequency,
which is inversely proportional to the air volume contained inside
the reverberation chamber.
Below this lower limit, the absolute results of the sound
insertion loss and sound transmission loss tests are not reliable,
but the experimental data can however be useful for comparative
tests. The shape of the cavity affects the modal distribution: the
more irregular, the more homogeneous the distribution. However,
more complex shapes tend to reduce the stiffness to weight ratio
of the structure, thus limiting its mobility and requiring higher
production costs.
On the other hand, the surface finishing influences the cut-off
frequency of the measurable frequencies. Finally, the dimension
of the opening window, which doubles as a sample holder for
insertion loss tests, influences the measurements because smaller
samples tend to resent more of the boundary effects. In other term,
it must be found a good compromise for the sample dimension:
the larger the sample, the more negligible are the boundary effects
and the more material is required in order to perform each test.
All of these factors will be analysed at great lengths in the
following.
Theory/Calculation
Insertion loss measurements
The sound insulation properties of a material can be indicated
by means of the sound transmission loss (STL) parameter. This
parameter, expressed in the dB scale, can be derived from the
acoustic transmissibility as follows.
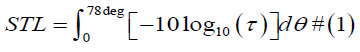
As an example, for a CLD sandwich with skins named 1 and 2,
can be estimated as follow
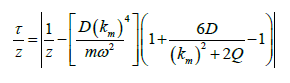
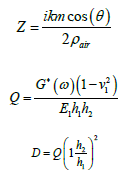
Where:
i. k is the wave number.
ii. θ is the integration angle that varies from 0deg to 78deg.
This particular value derives form numerical considerations,
as the contribution of angles higher than this are negligible to
the sound insulation properties of the panel [7].
iii. Z is the acoustical impedance.
iv. m is the surface density of the panel.
v. air ρ is the density of air.
vi. G∗ (ω ) is the frequency dependent complex shear
modulus of the core.
vii. h is the thickness.
viii. v is the Poisson modulus.
Theoretically, if all parameters are known, the STL can be
estimated from low-frequency rheological data by substituting
the frequency dependent shear modulus in the equation.
However, as this parameter requires a rather complex
numerical regression, it is possible to provide a first estimate of
the sound insulation properties of a polymer by extrapolating the
shear modulus form the measured STL spectrum. This spectrum
can be measured by means of a sound insertion loss (IL) test.
In this case, the test will be performed by employing
opportunely baffled samples inserted in a modified reverberation
chamber.
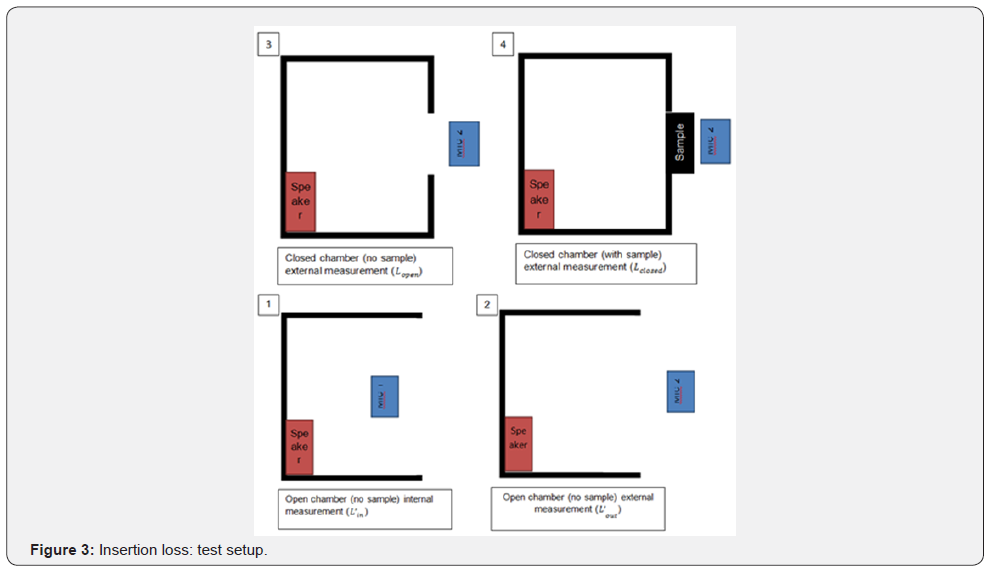
In general, the IL evaluation is based on the measurement of
the sound pressure field in four different configurations:
i. Front wall open + internal microphone in Lin'
ii. Front wall open + external microphone Lout'
iii. Front wall closed (no sample) + external microphone
Lopen'
iv. Front wall closed (with sample) + external microphone
Lclosed'
v. The sound transmission loss of the sample is equal to
(Figure 1 & Figure 2):
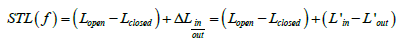

Preliminary considerations
The main global design prerequisites for the reverberation
chamber can be resumed as follow:
i. Minimal amount of space required for the whole
structure (accessories and base frame included).
ii. Minimal wall thickness imposed by the necessity of
sound insulation inside the chamber and stiffness of the
structure during the construction and transport phases
iii. Shape of the cavity motivated by the desire to homogenize
the natural mode distribution on the whole spectrum

iv. Maximisation of the internal volume in the chamber, in
order to minimize the lower measurement limit imposed by
the Schroeder frequency [7-10];
v. Minimum porosity of the internal surface, in order to
increase the cut-off frequency of the structure [11].
Before proceeding, it was considered as a minimum
acceptable frequency range for sound insulation measurements
2000-10000Hz, compatible with many engineering applications
of industrial interest, from an acoustical perspective.
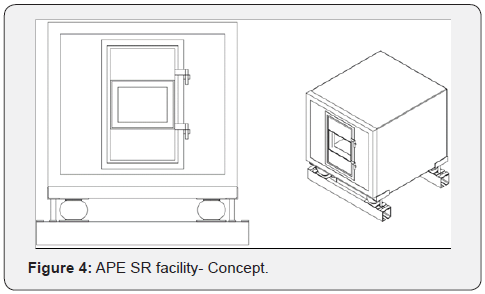
Taking into account the previously listed requisites, it was
chosen for the main body of the reverberation chamber a concrete
cube with a cavity on the front side (Figure 3). The front side
presents threaded wire for a secure attachment of the closing wall
or the second reverberation/anechoic chamber.

On a side note, even if opportunely shaped hexahedral
cavities were proven to provide a more uniform distribution of
the natural frequencies [12], the internal cavity of the APE SR
was shaped as a rectangular parallelepiped, because of the better
stiffness to weight ratio of the structure of the latter solution
and, as a consequence, higher manoeuvrability. For the base of
the reverberation chamber, it was chosen a frame connected to
pneumatic vibration isolators (4Hz cut-off frequency).
These last structural elements, interposed between the
frame and the main body of the reverberation chamber, serve
the purpose of decoupling the structure from the external
environment, in order to minimize the external influences (i.e.
floor vibrations, shaker induced structure borne vibrations)
during the measurement phase. The closing wall is fashioned
with the same goal of achieving a multi-purpose structure and
presents a movable inspection panel, with a detachable sample
holder, allowing a “clamped” boundary condition. We installed
ulterior threaded wires for attaching the measure apparatus
(i.e. omnidirectional microphone) and a secondary anechoic
chamber; both used in transmission loss (TL) and insertion loss
(IL) evaluations.
Design and optimization of the APESR facility
Staring from the solution of Helmholtz’s equation, it is possible
to evaluate the distribution of the modes of the system [13-16].
Taking into account the infinitely rigid boundaries, we can
assume that the wall specific impedance is infinite and the velocity
field at the boundaries is null.
In a Cartesian reference system with axis parallel to the sides
of the enclosed cavity:
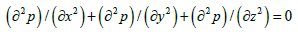
By substituting the trial solution p( x ,y, z) = px( x) py( y) pz( z)
into the wave equation(1), this is decomposed into three analogous
ordinary differential equations (ODE), where the only difference
is in the coordinates (x in the first, y in the second and z in the
third one). The same consideration is verified for the rigid wall
boundary conditions (BC). From now on, the discussion will be
focused on the first ODE and its BC (the one in the x coordinate),
but the obtained results can be easily inferred for the other two
equations.
The function Px , in order to be physically acceptable, must
verify the following conditions (2):
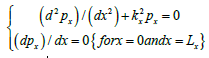
Where Lx denotes the base width, considering the origin of
the reference systemlocated in a vertex of the base rectangle.
The three orthogonal components of wave numbers k must
satisfy the following condition:
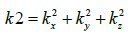
The solution of the first ODE can be written as: px( x)=A1cos(kxx=B1kxx)
In order to satisfy the imposed BCs, 1 B = 0
and Kx = (nx π)/ Lx
where nx is a generic natural number.
By substituting these last equations (and the analogous ones
for Ky and Kz into equation (3), we obtain:
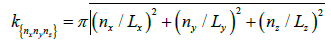
Associated to the eigenvectors, we can evaluate the functions:
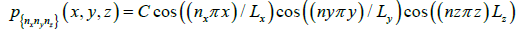
Where C is an arbitrary constant which satisfies the boundary
conditions.
Finally, the associated eigen frequencies of the air cavity are:
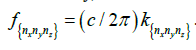
At this point, it is possible optimizing, from an acoustical
perspective, the shape of the cavity considering the following
constraints:
i. Maximum stiffness-to-weight ratio of the structure
ii. Maximum Schroeder’s frequency
iii. Uniform distribution of the eigenfrequencies
iv. Construction simplicity.
Taking into account the average distance between two successive eigenmodes

and the variation in frequency

of the Δf -nth eigen mode from the average value, this last constraint imposes the minimization of the index

, indicating the homogeneity in the distance between different mode shapes.
This constrained optimization was further refined by Blaszak’s
method [9,17], consisting in the minimisation of a secondary
index

This simultaneous constrained optimization, carried out
while taking into account the ease of construction of the structure
and other technological constraints, led to the design shown in the
following schematics (Figure 4):


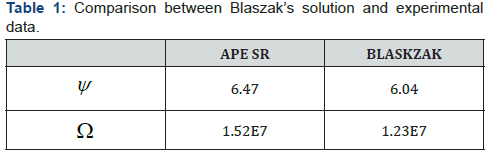
This results rounds down Blaszak’s proportion fora
reverberation chamber with walls characterised by an average
acoustic absorption of α ≈ 0.01(1:1.2 :1.4). The differences between Ωψ for the two solutions are shown in the following table
(Table 1):
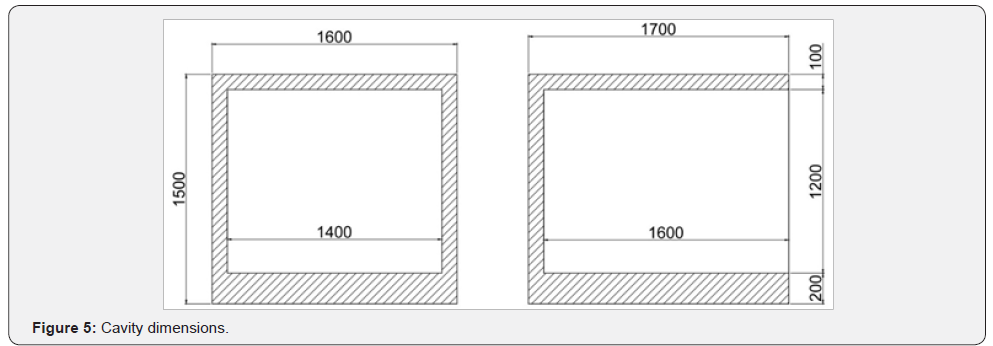
The differences between the proposed design and Blaszak’s
optimised design in terms of eigenmodes distribution can be
shown in the following graph (Figure 5). The graph considersa
hypothetic reverberation chamber with internal dimensions of
1.20mx1.44mx1.68m (which accords to Blaszak’s proportion).
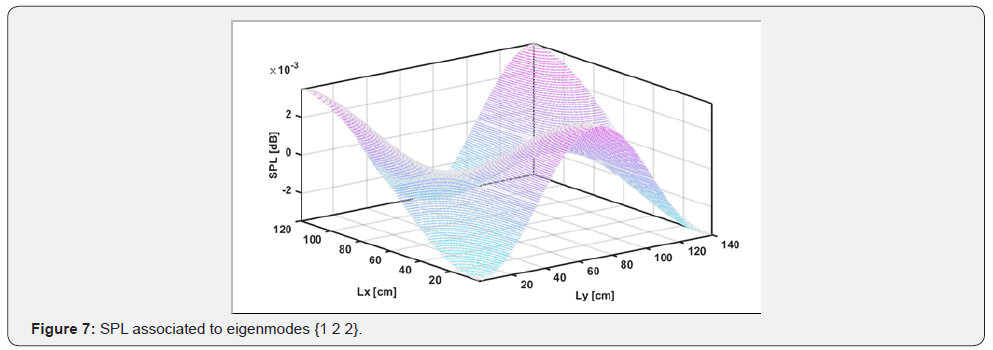
By substitutingthe eigenmodes inside the Helmholtz’s equation,
it is possible to evaluate the acoustic pressure field for the various
eigenmodes. For example, in the following Figure 6, it is shown the
sound pressure level (SPL) in the x-y plane at z=50 [cm] associated
toeigen modes {1 2 2}.


From a merely qualitative perspective, it can be noticed that
the regions where the sound pressure level is null coincide with
the projections of the nodal planes on the x,y plane. In conclusion,
the acoustical design parameters can be summarized in the
following (Table 2).

Construction of the sound research facility
The material chosen for the construction of the reverberation
chamber was reinforced concrete, because of the low cost,
low acoustic absorption and high density. This last parameter
influences the acoustic insulation properties and the seismic
mass of the system: the higher the density, the better the sound
insulation. The reverberation chamber was manufactured by
using a mix design of Portland cement (type II/A-LL 45,2R) and
finely grinded sand which was compacted both by ultrasonic
means (needle compaction) and external means (vibrating plate
compaction). This process was carried out in order to maximize
the sound reflection and minimize the absorption caused by local
Helmholtz resonator effects.
This acoustical mechanism can be traced back to the microporosities
naturally present in concrete-based structures. In
order to reduce the sound absorption of the concrete, the interior
of the cavity was furtherly coated with a thin layer of stucco. The
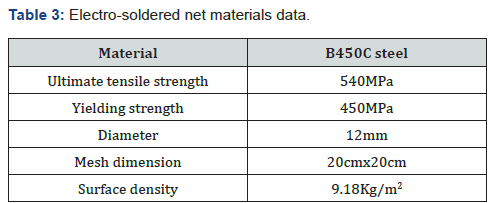
concrete was reinforced with an electro-soldered steel net with
the following characteristics (Table 3).

Because of the necessity of rotating the structure once the
concrete dried, the reverberation chamber was designed with a
reinforced bottom, with two electro-soldered nets Figure 7 and
an increased wall thickness of 200mm [18]. The structure was
removed from the mould after 2days and the concrete was left
to maturate for 30 days before the rotation (see rotated APE SR
in Figure 8), in order to increase its compression strength up to
42.5MPa and to minimize the risk of failure.


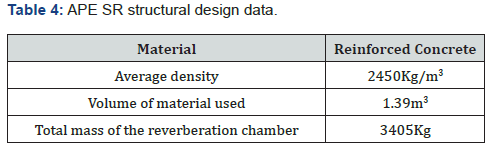
The design data can be resumed in the following table (Table
4):

In order to decouple the dynamic response of the reverberation
chamber from the floor vibrations [19-21], for the suspension
system were used 4 pneumatic suspensions (Figure 9), each one
with a load bearing capability up to 1600kg at 7 bar [22]. The
whole assembled structure is shown in the following (Figure 10).


The schematics of the reverberation chamber, excluding the
sample holder and inspection panel, is reported in (Figure 11).
In order to validate the chamber and the measuring system
different materials were used.

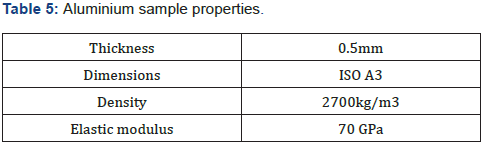
In the case of insertion loss, instead, an aluminium alloy
plate Al 6060, with the following characteristics (Table 5) was
employed:

Finally, after chamber validation, measurements of a sandwich
in constrained layer damping configuration, were carried out in
order to assess its acoustic properties. At this regard, the damping
layer was prepared by mixing a Polyethylene Glycol 200g/mol
(Sigma Aldrich) with a 20% by weight of 12nm fumed silica
(Sigma Aldrich), while the outer skins were two plates of Al6060
with a thickness of 0.5mm.
The colloid was prepared by recurring to the following
approach [23]:
i. The powders were dried in an unventilated oven (8h-50
°C).
ii. The powders were dispersed in intermediate carrier
and the resulting slurry was subsequently dispersed in excess
solvent.
iii. The slurry was magnetically stirred at ambient
temperature and then in an ultrasonic bath.
iv. The agglomerates were dispersed in the carrier fluid by
jar-stirring.
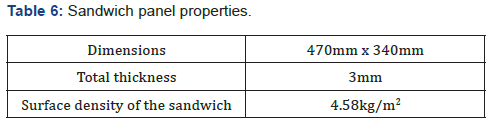
The sandwich used exhibits the following characteristics
(Table 6).

Experimental
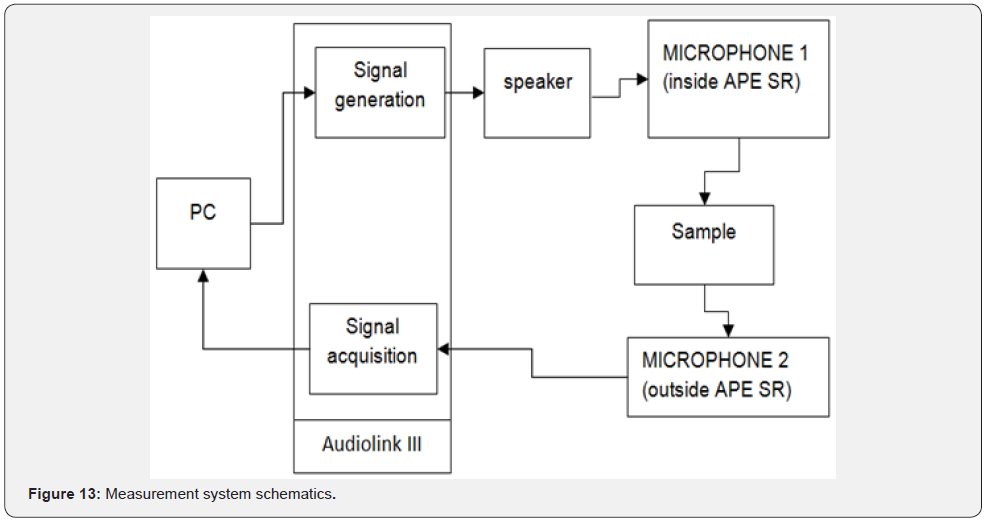
The measurement system annex to the facility and used in
the various acoustical characterisation (insertion loss, absorption
loss) consists of:
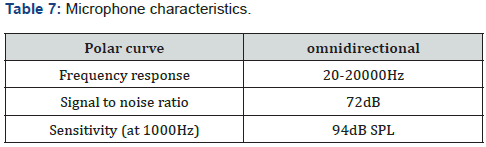
i. Two laboratory microphones Super lux ECM 888 B ¼’’
with the following characteristics (Table 7).

ii. An 80-watt speaker with a flat frequency response
(without a prevailing frequency content) between 50Hz and
20000Hz.
iii. A dual mode acquisition card Midtech Audiolink III (two
microphone input-ports and a STEREO or dual MONO audio
output-ports).

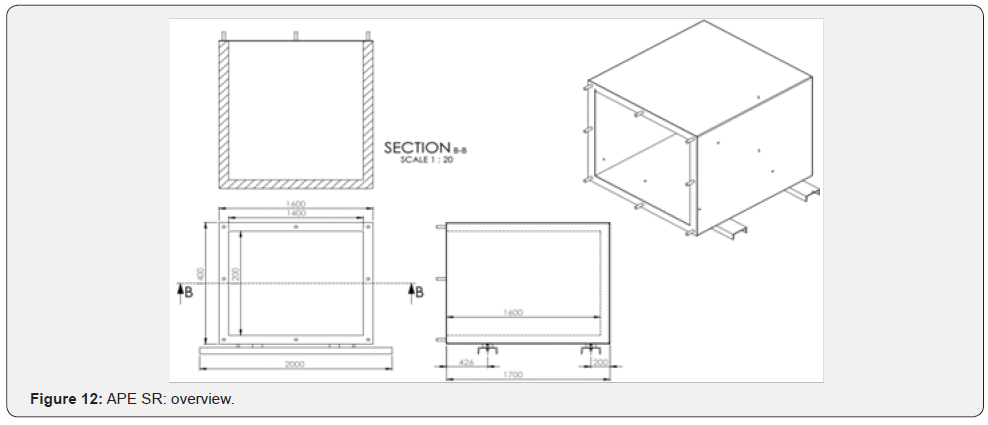
The measurement system (Figure 12) is connected as follows.
The proposed design of the APE SR reverberation chamber
was validated and compared to the previous analytical results.
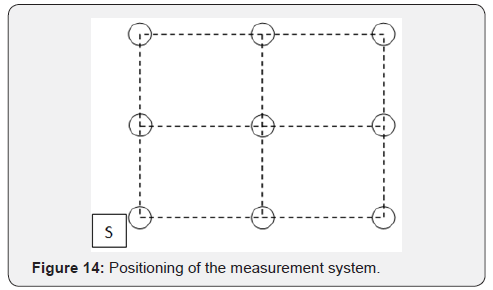
The speaker was located in a fixed position while the microphone
was relocated in 9 different positions (indicated as white circles
in the following Figure 13) in the x-y plane at the same height
z=h/2=1200 mm/2=600mm. During the validation, the sample
holder was momentarily closed with a concrete panel and
completely sealed with a layer of sealant.

The input signal generated was a sine sweep wave with a
linearly variable excitation frequency from 20Hz to 20kHz and
constant unitary amplitude, maintained for 10seconds. The
effective SPL inside the chamber was recorded by the microphone
in each of the 9 configurations and post-processed with the
commercial software Fuzz Measure.
The post-processing is divided into the following phases:
i. Deconvolution of the audio signal, in order to evaluate
the system response to the excitation wave.
ii. Fast Fourier transform (FFT) of the time history data, in
order to evaluate the response in terms of frequency and SPL
[dB].
iii. Evaluation of the actual reverberation time of the
structure and its dependence on frequency.
The Deconvolution is necessary to evaluate the response
of the system to the excitation, in order to filter the signal from
the background noise innate to the measurement system and to
calculate the FFT. This allowed us to evaluate the SPL in 9 different
microphone positions (indicated by the thin coloured lines) of the
reverberation chamber.
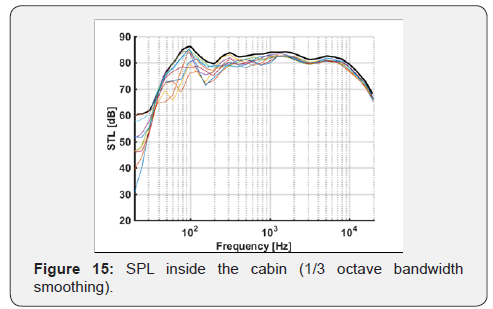
In the following graph (Figure 14), the envelope of the 9 curves
is represented by a bold black line. The signal was smoothed
choosing 1/3 octave bandwidth smoothing (Figure 15).


By observing the data, it can be acknowledged the existence
of a region approximately below 100Hz where the SPL inside the
chamber reaches a minimum. This is caused by the first resonance
of the chamber, which occurs at approximately 106Hz. Before this
frequency there are de facto no reflexions and the sound pressure
level varies significantly from point to point inside the chamber
and assumes low values. Between 100 and 500 Hz the SPL is
highly variable from point to point and the response is highly
dependent on frequency: this is caused by the higher eigenmodes.
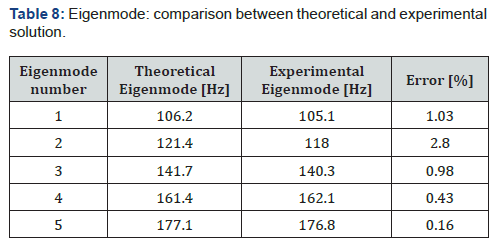
By analysing the envelope of the SPL curved, it is possible
to compare the theoretical eigenfrequencies, calculated by
Helmholtz’s equation, and the experimentally measured ones
(Table 8):

Roughly above 700Hz the SPL envelope curve approximates
a quasi-linear trend and the nine curves tend to coincide. This
phenomenon is an indicator of the fact that the sound power
inside the chamber is almost constant above this frequency. As
a consequence, this signals the passage from a system whose
dynamics are dominated by its modal response to a more desirable
condition of diffused acoustic field.
Also in this case, there is good accordance with the theoretical
value for Schroeder’s frequency. Taking into account that 1000Hz
is the central frequency of the octave bandwidth 710Hz-1420Hz,
we can notice graphically that the diffused field in the APE SR
facility occurs approximately between 700Hz and 1000Hz: this
limit denotes the inferior limit of validity of the successive results
for the STL of the tested samples.
As it can be noticed, between 9000Hz and 20kHz the SPL
decreases, even though it is still maintained the diffused acoustic
field condition. This reduction in the SPL is caused by the microporosities
in the concrete, which act as microscopic Helmholtz
resonators at higher frequencies.
This variation is however limited to 2-3dB up to 15kHz
and, therefore, can be considered negligible. Because of the
complexity associated with the calculation of the reverberation
time RT60, it was chosen to extrapolate this parameter from the
T20, a conceptually analogous parameter, which is evaluated for an
attenuation of 20dB instead of the 60dB required for the previous
parameter. In fact, in order to calculate the RT60 it is first necessary
to calculate time necessary to have a 60DB attenuation in the
sound energy density D(t) [dB].
However, even though theoretically possible, the calculation
of this value is nontrivial, in particular in small room acoustics
where the dynamic range, nominally the difference between
the maximum value of D(t) and its asymptotic value, is much
smaller than 75dB. This particular value has been demonstrated
empirically [24] to be the threshold value of this parameter
necessary to actually measure and attenuation of 60 dB and
therefore, to evaluate, the RT60. Therefore, according to the norm
ISO 3382, the reverberation time was calculated basing on the
evaluation of a parameter requiring an inferior dynamic range.
The starting point for the refining of the analysis was the
measurement of D(t)=20 log(h(t)/max[h(t)]) where h(t) is the envelope
of the excitation H(t).
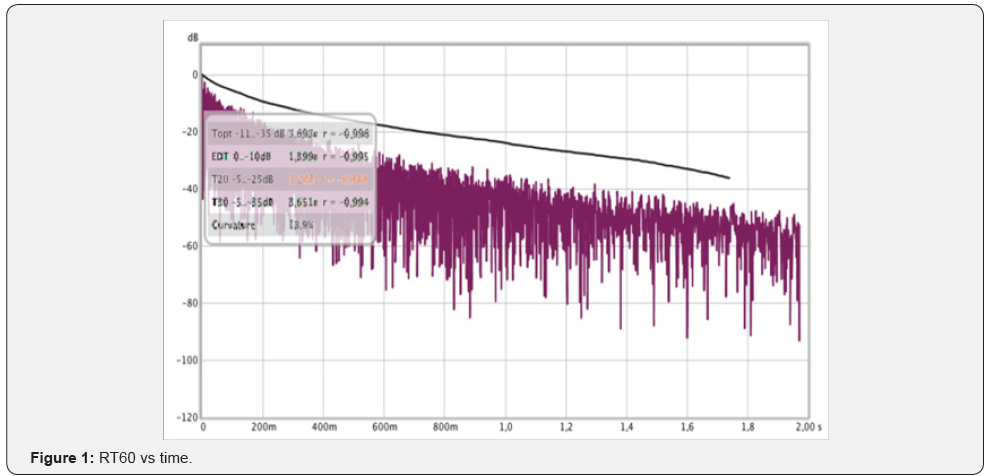
D(t), represented as a thin purple line in the following picture
varies between 0 dB and the value corresponding to the sound
energy density of the background noise.
On the other hand, the Schroeder’s integral

is represented as a bold black line in the graph.
From Schroeder’s integral, it is possible to derive a linear
extrapolation of the reverberation times, by considering a linear
relationship r = A∗t + B ,where A is the slope and B is the
expected attenuation.
Therefore 60 RT = −60 / A, where A is evaluted from the
experimental measurement of the T20.
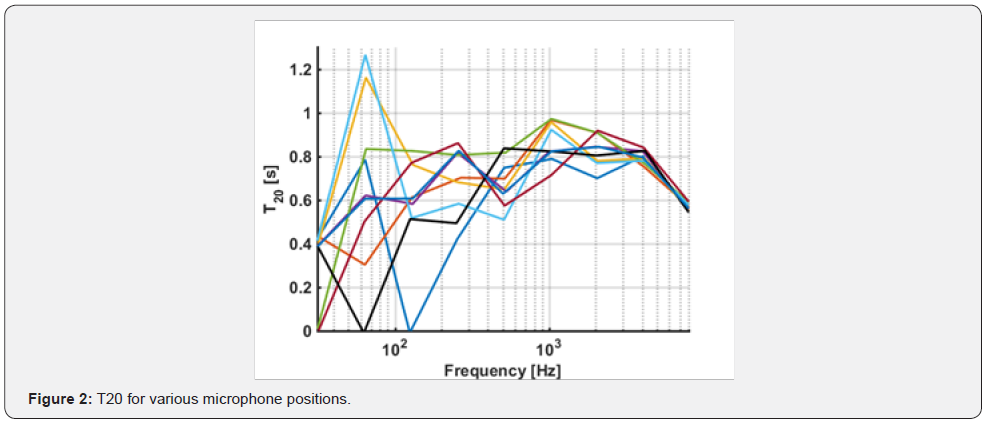
The results for the T20for the various positions of the
microphone at the centre frequency for each octave band width
can be shown in the following graph (Figure 16):

The extrapolated experimental value for RT60 is 2.34s, which
coincides with the value theoretically expected from Sabine’s
formula.
Results and Discussion
The first step to evaluate the sound transmission loss of
the system was the evaluation of the system in the first two
configurations. The samples were all be tested with the baffled
boundary condition and a white noise signal (a random signal
having a constant power spectral density). This value is an index
of the influence of the closing wall to the sound pressure level
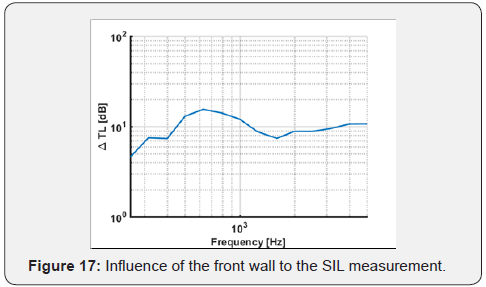
effectively perceived by the sample (Figure 17). The results with a
1/3 of octave bandwidth smoothing showed that this value attests
at around 10dB after the diffused field condition is established.
This parameter is extremely relevant in the case of the APE SR,
because of the reduced size of the sample holder, which causes a
non-negligible boundary effect contribution to the IL.

For the proposed design, the minimum sample dimension
was reduced to a ISO A3 standard, much smaller than the 6m2
required for traditional transmission loss testing and therefore
this parameter is non-negligible to the system response. Once the
system was set, it was possible to compare the numerical expected
results for a simple system, whose vibroacousticresponseis widely
known in the currently available literature (i.e. aluminium plate)
with the measured ones.

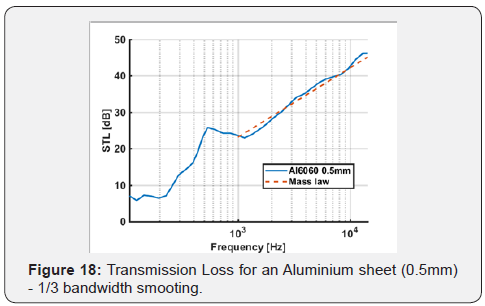
As it can be seen (Figure 18), the experimental results are
adherent to the theoretical ones in the diffused field region, as
expected. We can therefore consider the system fully validated
and we can consider reliable the results for our measurements
between 700 and 15000Hz. Below 700Hz, as previously discussed,
there is a highly instable zone characterized by the presence of
both the modal response of the chamber and of the resonance of
the material.
However, it is still possible to identify the stiffness-controlled
zone of the response of the system at approximately 100Hz and
the damping-controlled zone between 200Hz and 1000Hz, as
expected by the theoretical results [25-28].
With the fully validated system, the same analysis was
repeated, as a proof of concept, for a sandwich structure in
constrained layer damping configuration, realized as previously
described in the Materials section. First of all, we carried out the
rheological analysis of the nanocomposite previously described,
by recurring to the following rheological approach.
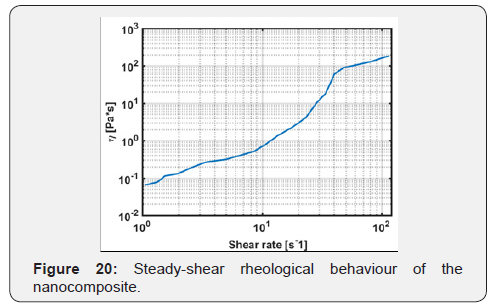
We carried out an steady-shear rheological measurement
with a Strain-controlled rheometer (Kinexus LabPro+). The
chosen fixture was a conical plate with a 0.8mm gap between the
sample and the lower end of the fixture. A 1 minute 1s{ 1} − shear
rate was applied to each sample (25ml), to break-pre-existing gel
structures and therefore, to be able to neglect pre-existing stress
fields in the fluid. The shear strain varied between 1 % and 120
%. This allowed us to pre-screen the properties of the fluid that
exhibits a shear-thickening Non-Newtonian behavior (Figure 19).

However, as these materials are rheologically complex and do
not obey to Delaware-Rutgers’ rule [29], to fully model the acoustic
constitutive behavior of this material requires further research.
Furthermore, Time-temperature superposition techniques, such
as WLF, generally provide unreliable constitutive behavior at
higher frequencies [30,31].
In order to fully model and analyse the vibroacoustic response
of the sandwich at acoustic frequencies and the dependence on
the composition of the nanocomposite, further investigation is
required for the rheological response of the polymer at acoustic
frequencies [1,32]. By iterating the Insertion loss measurement
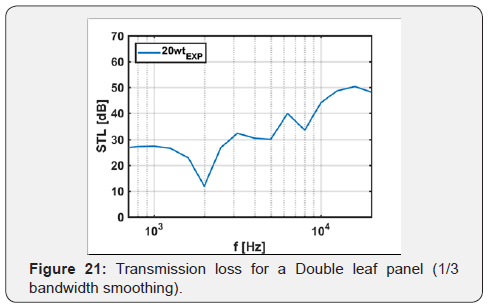
method reported above, it was possible to calculate the sound
insulation properties for the proposed sandwich material (Figure
20 & 21):


Between 2200Hz and 10000Hz shows a step increase in the
STL, before experiencing a progressive decrease in the sound
insulation properties. This is caused by the high-frequency
response of the proposed material composing the constrained
damper [7,33-36]. The decrease in the STL of the sandwich can
be ascribed to the reduction in the damping of the core at higher
frequencies, which occurs in the sandwich nearby the coincidence
frequency. In this range its response is actually dominated by the
damping of the system, in accordance with the previous results.
Finally, the complex shear modulus can be derived from the
STL. In both cases, as typically expected for STFs, the complex
shear modulus increases with frequency. As a comparison, the
results for the numerical extrapolation proposed in [23] are
compared with the ones extrapolated from equation 1 in (Figure
19). The linearly extrapolated shear modulus provides a good
matching with nonlinearly extrapolated one for lower frequencies.
However, the values tend to deviate from one another as the
frequency increases. This can be traced back both to errors in the
non-linear regression and in the experimental measurement, that
tend to increase at higher frequencies. Further research is due.
Conclusion
The objective of this work was the development of a empirical
approach to evaluate the rheological behaviour of smart materials.
This method required the design of a small acoustic research
facility, optimized for laboratory environments and quality
assurance laboratories.
The structure was designed as a flexible tool, usable for
the evaluation of the sound insulation of innovative composite
materials in diffused sound field conditions, which cannot be
achieved in conventional acoustic laboratory equipment such
as impedance tubes there are standard test methods for the
determination of these properties. There is, however, no standard
for the equipment used in these tests, only a specification for
the test conditions. The objective of this work was to evaluate
the operation and performance of a bench top laboratory sound
testing system for its potential as a simple cost effective method
for the initial evaluation of materials that require specific acoustic
properties. The work was limited to an investigation of the
property of sound transmission loss (STL(6)(6)(5)(5)(6)(6)(6).
As a consequence, the structure was designed taking into
account:
i. The maximisation of the stiffness to weight ratio of the
structure and its movability
ii. The reduction of the required dimension of the samples
(from 6m2 to an ISO A3).
iii. The maximisation of the frequency ranges of analysis, up
to 700Hz-15000Hz.
The reverberation chamber, built in reinforced concrete
according to these guidelines, was validated by testing the
insertion loss of an aluminum alloy plate Al 6060. The achieved
results showed a good agreement with datasheets of investigated
samples.
Further experimental tests demonstrated the potential
use of the chamber to assess the vibroacoustic behavior of
structures comprising smart materials. At this regard, preliminary
measurements carried out on a system constituted by aluminum
skins and a core including fumed silica nanoparticles highlighted
interesting perspectives of the new acoustic facility to investigate
nano structured systems that can be used as damping materials
as well as its actual reliability. Finally, the complex shear modulus
extrapolated from acoustical data was compared with the one
obtained by means of non-linear regression of rheological data
from low-frequency data.
For more
details Academic
Journal of Polymer Science please click on: https://juniperpublishers.com/ajop/index.php
To read more…Full Text in Juniper Publishers click on https://juniperpublishers.com/ajop/AJOP.MS.ID.555557.php

Comments
Post a Comment